|
Abstract
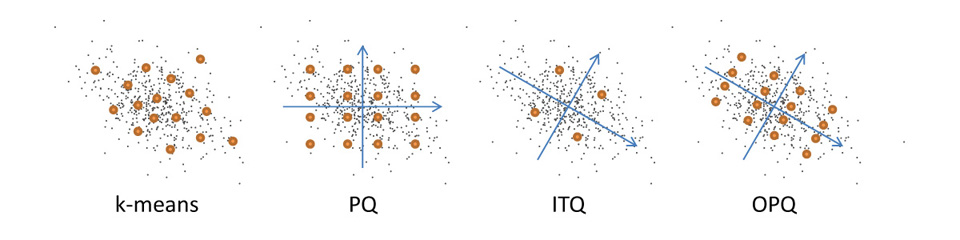
Product quantization (PQ) is an effective vector
quantization method. A product quantizer can generate an
exponentially large codebook at very low memory/time cost. The
essence of PQ is to decompose the high-dimensional vector space into
the Cartesian product of subspaces and then quantize these subspaces
separately. The optimal space decomposition is important for the PQ
performance, but still remains an unaddressed issue. In this paper,
we optimize PQ by minimizing quantization distortions w.r.t. the
space decomposition and the quantization codebooks. We present two
novel solutions to this challenging optimization problem. The first
solution iteratively solves two simpler sub-problems. The second
solution is based on a Gaussian assumption and provides theoretical
analysis of the optimality.
We evaluate our optimized product quantizers in
three applications: (i) compact encoding for exhaustive ranking ,
(ii) building inverted multi-indexing for non-exhaustive search, and
(iii) compacting image representations for image retrieval. In all
applications our optimized product quantizers outperform existing
solutions. |